What is Base64?

What is Base 64 Encoding?

Introduction

Base64 encoding is a format designed to prevent communication “mishaps” during the transfer of binary information. It achieves this through the conversion of binary data and a “lookup table” — data is eventually made in a stream of ASCII characters, which can then be transmitted and decoded. On base 64 encoded data, the resultant string is always larger than the original (i.e. this is not a compression algorithm). Another important distinction is that base 64 does not encrypt any information — it uses a “standard” table of characters to encode and decode information. In other words, any base-64 string can be decoded, as long as the string was encoded using a standard set of characters (which the decoder can also understand).

Uses for Base64

On top of being used for safely encoding image/media data (you may have seen images on the web encoded in the following format: data:image/png;base64,(...)), it is used for SSL certificates, email transmissions, and virtually any transfer of information that requires special (control) characters to be escaped.

Encoding Base64

While many programming languages (e.g. Java, Python, JS) include built-in functions to facilitate the conversion of base64 encoded information and binary data, the algorithm used to perform the conversion is relatively simple. Starting with binary information, base 64 splits a binary string into 6-bit groups (note: each zero or one in a binary string is one bit) of three bytes. The result is an ASCII-readable string that can be safely transmitted and received.

For the sake of simplicity, we’ll use a short string to demonstrate the encoding process. Suppose we have “hi” as our string, the ASCII equivalent being: 104 (h), 105 (i).

We need to convert the ASCII string to its binary representation:

01101000 01101001 (0110100001101001 without spaces)

Now, divide the binary representation into 6-bit groups:

011010 000110 100100

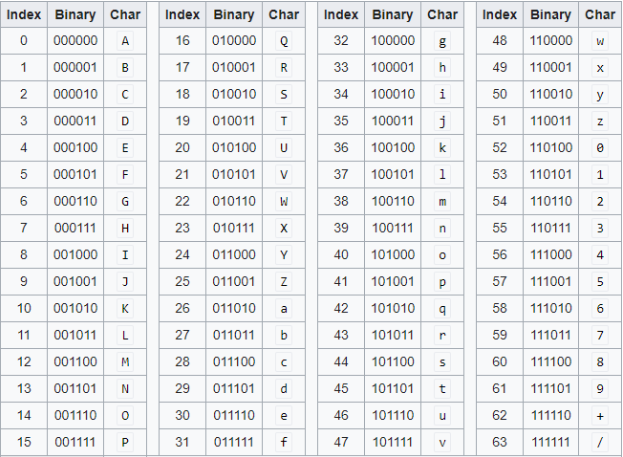
With the binary representation of our string, we can then make use of an ASCII lookup table above. We get the following ASCII characters for our string’s binary representation:

• 011010 => “a”
• 000110 => “G”
• 100100 => “k”

Before we can finish off the conversion process, it is important to notice the missing padding: base 64 strings must be groups of 3 characters (6 byte binary representations). As such, our string “hi” only has 2 characters; this means that we need to insert a “=” at the end of the string to make this a valid base 64 string.

The result is finally: “aGk=” (hi).

Decoding Base64

Decoding base64 strings follows a similar process, just in reverse. Using the result from the previous section (“aGk=”), we will use the same Base 64 lookup table:

• “a” => 011010
• “G” => 000110
• “k” => 100100
• “=” => padding

This leaves us with three 6-bit binary groups:

011010 000110 100100

Converting this back to 8-bit groups, we get (the last two zeroes can be ignored):

01101000 01101001

… which results in “hi” in ASCII.

Conclusion

Whether you’re sending an email, or trying to encode binary streams (images, videos, etc.), base 64 can be seen in many applications. While the resulting strings are larger, using base 64 encoding is a reliable way to ensure that a transmission of binary information is never “misinterpreted.”